level set （水平集）算法是什么？

一年前看到师兄弄 level set，当时没有看懂。

前几天，在看一本书时，偶然又看到这个，就打算来仔细了解一下了。

所以，下面的这些点子新鲜出炉的，没有太多的实战经验，若有错误，应该也是很正常的，请见谅。

这篇答案，最大的启发来自youtube的这两个视频：

--------------------------------------------------------------

1.

我第一次看到 level-set 的时候，我认为它是一种图像分割的方法。

当然，大家也都这么说。

不过，从这几天的了解来看，如果在内心一直带着“它是一种图像分割方法”这个想法，反而是带着一些框框，很多概念变得不那么好理解了。

所以，第一步： 请忘掉这件事情，暂时我们不说它是一种图像分割的方法。

2.

在说 level set 之前，我们先谈 曲线的演变。

我们已经有一条曲线了。

现在，假如我们要演变它。

这里的意思是，我们要让一条曲线变化，慢慢地变成另一条曲线。

那么我们很容易想到的一个点子是：我只需要指定曲线上的每一个点的运动方向和速度就可以了。
可以参考下面这个图：

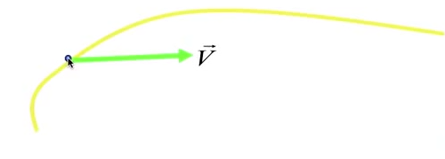
这个图里面只考察了一个点的运动方向和速度。

3.

到这里可能会很让你惊讶。

我们还没有提及到任何 和 “level -set” 有关的东西，图像分割的点子已经来了。

图像分割的结果是，在我们要分割的图像上，我们绘制了一条曲线。

曲线包住了一些东西，那被我们说成是分割出来了的东西。

所以，图像分割，如果用曲线演变的方法，大约就是在要分割的图片上，先随便绘制一条曲线，然后让这条曲线演变成我们想要的曲线，分割就搞定了。

回看一下上面，曲线的演变的话，我们其实只需要控制的是每一个点在每一个时刻的速度而已。

图像分割，仅仅是，针对曲线上的每一个点，考察其盖住的图像，通过此来决定在曲线上的这个的点的运动速度而已。

为了说明，我打算举个例子：

上面图里，那个红色小圈就是我的初始曲线。

现在，我要演变这个曲线。

那么也就是要控制每一个时刻这个曲线上的每一个点的运动速度和方向。

方向嘛，我就朝外（arc length 法线方向），而大小呢，我就根据这条曲线盖住的图像来确定。

（把图像和曲线看成在两个不同的图层，曲线在上一层，图像在它下面）

这个大小的确定有很多不同的方法，但是很基本的要满足的条件是：我希望到快接近边缘的时候，速度就慢了，甚至停了下来，而如果曲线上的那个点不靠近边缘，那么速度就得比较快。

比如说，大小确定的方法，我根据曲线上的每一个点，当前盖住的图像的点处的梯度来决定速度的大小。

如果梯度比较小，那说明这个时候，曲线还在肚子里面，我的速度就可以大一点。

如果梯度比较大，那么说明这个时候，已经接近了边缘了，那么我的运动速度就要小一点了。

因此，曲线上每一个点运动的速度，和其盖住的图像的点的梯度大约成反比：

比如上图，绿色的点的运动速度就很大。

而黄色的那个点啊，就得运动得很慢了，甚至几乎不怎么运动。

慢慢地，这个曲线就贴近图像的轮廓了。

至少从我目前的理解来看，核心在于如何通过要分割的图像，去确定曲线运动的速度。

4.

图像分割的故事其实已经说完了。

到目前为止，都还没有说到 level - set。

小结一下： level set 准确地说来，不是图像分割的方法。

真正的图像分割的方法，是 曲线的演变。

我们通过把每一个点的演变速度和图像扯上关系，曲线就慢慢演变成了轮廓。

那 level-set 是什么？它是 曲线演变的 实现方法。

5.

上面的曲线演变，在真的实现的时候，会很头疼。

所以，才需要 level set 帮忙。

在这个部分，我打算谈一下是怎么头疼的：

（1）绿色曲线的两个邻近的点，根据当前的速度演变，到了下一刻，成了红色曲线上的两个点。注意到，这里曲线“变长”了，多出了蓝色的点，这个点还需要插值出来得到。

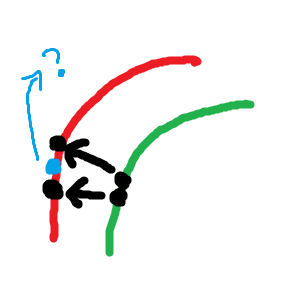
（2）

对于左边的图，如果是从红色曲线演变成黄色的曲线，其实好比较容易想通。

但是，从黄色曲线演变成红色曲线就有点费解了。

因为有的地方，两个点重合了之后，不知道该如何描述下一个时刻。

是两个点和成了一个呢？还是每一个点都还有自己的运动。

再看右边，红色曲线很光滑，慢慢朝着里面运动，变得越来越尖了。这个时候又不好描述点的运动了。

所以，真的去跟踪每一个点的运动是很头疼的。

6.

终于要说到 level set了。

先来看这个词，set 的意思是集合。

我们要描述直线上的两个点，那么可以直接就写出两个点的坐标：

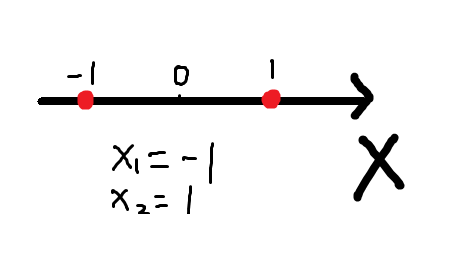
你也可以绕一下，写成集合的形式，也就是所谓的 level set：

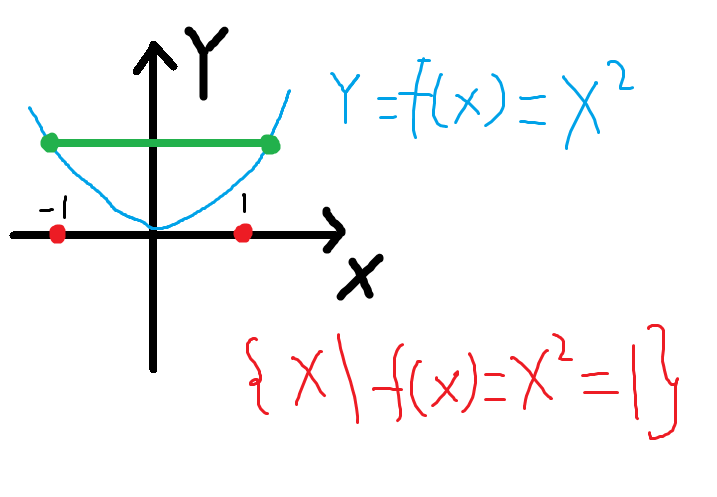
这里的 y 的取值就是 level，那么和上面相比，直接是X 轴上的两个点。

在这里的话，表达方式就成了，level 为1 的所有x取值的集合。

所以对于曲线来说是一样的。

一个曲线是二维的。

我们可以直接用一个参数方程在二维平面上表示一条曲线：

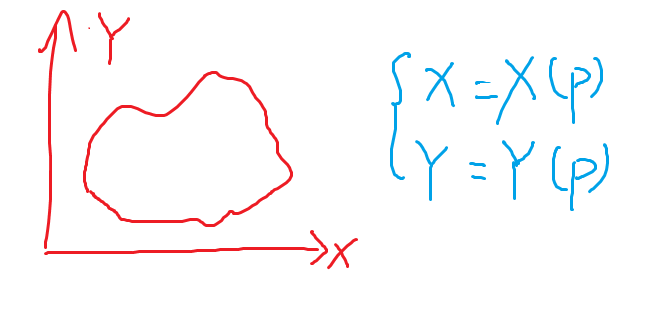
或者，也是表示集合的形式，那么就会是一个曲面（二元函数）上，某个level下的（一般选择的是level=0，也就是 f(x,y)=0），所有点的（x，y）坐标的集合（图中红色的为曲线，这些点的z坐标均为零）：

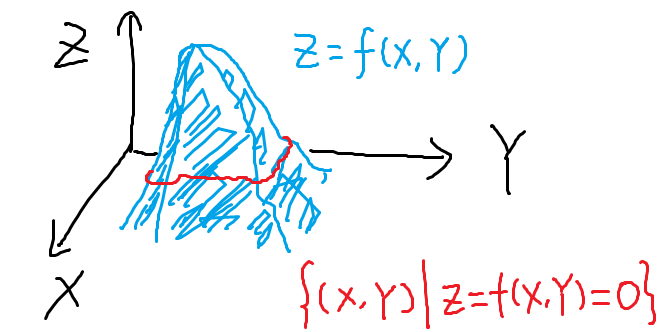
7.

于是，上面的曲线的演变，可以变成了这个 f(x,y)随着时间演变，整个曲面发生了变化，它的level 0 的集合（即曲线），也发生了变化。

说是这么说，到底能不能实现，就需要回到我们上面曲线演变的问题：

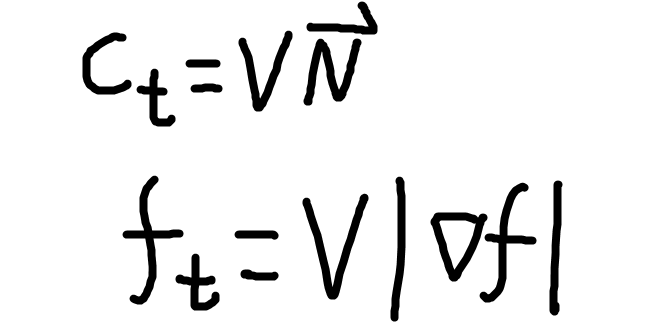
上图中的第一个公式，其实就是对于我们上面曲线演变的描述。

C表示的曲线（这里省略了具体细节，用这个比较模糊的式子，实际上为 C(p)=(x(p),y(p))），下标t表示，C对t求导。那么这个实际上，得到的是曲线上的每一个点的运动速度（向量）。

所有右边的V是速度的大小，而N是指的曲线的法线方向。

这里是我不太懂的地方，视频的作者不断谈到，改变曲线形状的速度方向是法线方向的，而切线方向的速度是不改变曲线的形状的，所以，在曲线的演变中，所有的点都只考虑了其发现方向的速度。

然后下面一个公式，f是一个二元函数，以x和y自变量的函数，它的取值为零时，所有的

x和y的坐标点的集合就是我们的曲线，它是第一个式子通过推导（其中需要引入的条件就是，level=0 时的集合为曲线）得来的。意思是说，你的曲面只要按照这个式子去演变，那么其level 0，总是我们想要的曲线。

所以，来回顾一下：

我们要实现的是第一个公式，曲线的演变，其中的V怎么来选择，我们暂时不管，V选择的方式才决定了我们要干的事情是不是图像分割。

而第二个公式，是曲面的演变，曲面的演变，如果遵循这个式子，即是曲面上的点，z=f(x,y)的取值，随着时间的变化满足这个式子的右边。那么每一次，取这个曲面的 level 0，那些点就一定是上面我们想要的当前状态下的曲线。

再来看下第二个式子要怎么实现？

很简单。

一开始，随便选取一个曲面，只要其 level 0 为我们要的初始曲线。

然后，下一刻时刻，仅仅根据V，还有当前曲面的梯度，就能得到 f_t.

然后，把所有的z的取值，都加上对应的 del*f_t 即可。

非常容易。

完全不用再去考虑曲线的每一个点怎么运动的了。

其实 Level Set 就是地形图上常见的等高线：

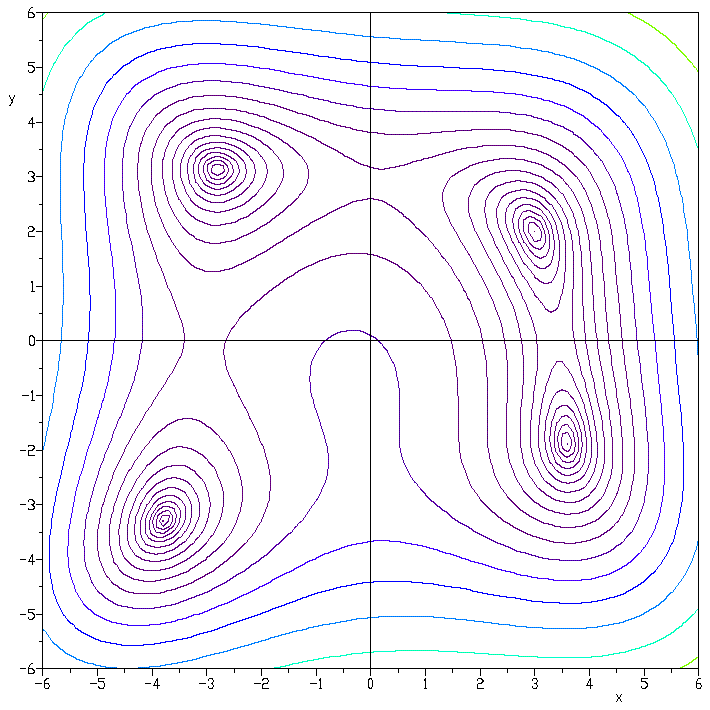
而 Level Set Method 就是通过连续上下移动等高平面（下图中的蓝色平面），得到连续变化的轮廓，从而模拟曲线或曲面的连续变形。

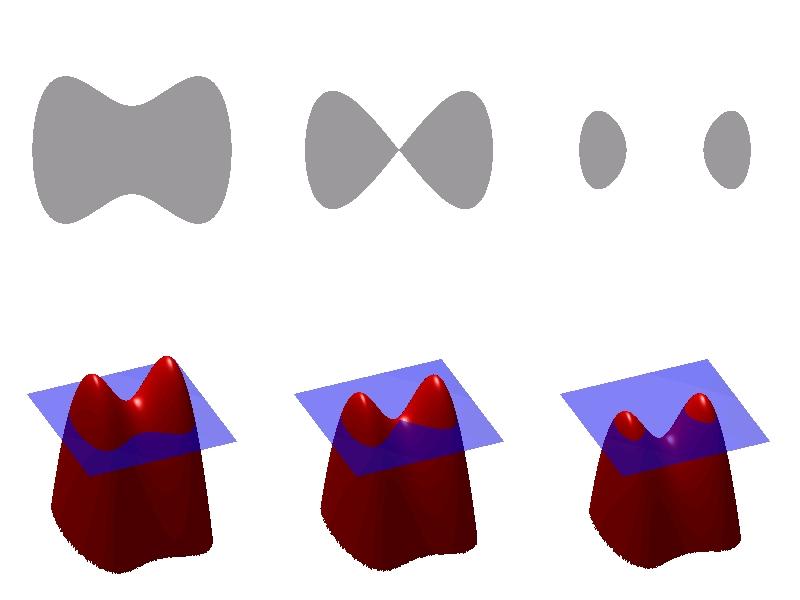
图片来自维基百科：

首先必须要赞一波水平集的鼻祖们，这个方法确实牛，用形象的数学工具表达目标，还可以方便的在能量泛函中加入先验知识，确实高明。

其实维基百科说的也差不多了。水平集算法是一种隐式的表示曲线的方法。就是把低维目标用比他高一维的水平集函数的零水平集来表示。零水平集可以有很多个曲线来表示目标，这就得看你的目标是什么样子了。说完水平集函数，就要说你构造的能量泛函了，这个函数一般都有一个内部力量项，外部力量项和一个正则项。怎么构建的？具体看各个文章了，大多都是差不多的，手机也不好搞公式…（主要是懒）这又牵扯到泛函。我们一般说的函数是关于变量的，而泛函通俗讲就是关于函数的函数， 水平集方法构建的能量泛函就是关于水平集函数的。当极小化这个泛函时，水平集函数的零水平集也就收缩到目标边界。这是因为零水平集受到内力和外力作用，当和目标重合时，内外力平衡，能量极小化。

……………………分割线………………………

水平集常用在活动轮廓active contour 方法中表示曲线，而活动轮廓又分为基于区域的和基于边缘的方法。安利一个大牛，李纯明，现在回国了，之前就是看他的水平集文章，有两篇都是best paper。其中基于区域的方法可以看李纯明教授的RSF，写的很好，不依赖于初始化，还有相关代码也公开了。基于边缘的方法可以看他的DRLSE，对初始化敏感，但是对简单图效果很好。这两篇看完如果还很迷糊，当然我也迷糊。。。你可以再去看看蛇模型和CV，看看区别，总结一下，感觉就可以了，有些东西说是说不粗来的。

记得有个老师讲课时候说，我们搞图像的，经常被别人说我们的算法都没有普适性，都是需要靠人品的，人品好了，参数调对了，结果就有了，没人品，对不起。。。

简单来说就是一个沿着他的法向演化的曲线。因为最简单的level set函数就是

\\frac{\\partial{\\Phi}}{\\partial t}=|\ abla \\Phi|，

当然用在图像里面实际上就是用一个二维函数（比如signed distance function)来表示当前的分割结果（即0水平集）。所以这样你就可以区分外部或者内部（就是H(\\Phi),H是Heaviside函数）。这样比如对普通的模型，比如CV模型，你求变分极值出来实际上就是我上面说的那个方程。当然会复杂一些实际问题。

我来写点东西

其实之前讲解的level取0，那么为啥要取0和为什么最后会到0呢？？？我个人理解，其实就是让我们的函数三维的没有第三维。这样写比较方便，也很好被接受x2+y2+1=0，这样多好看。

然后我要说的是，我们在变化的时候我们的水平没有变，其实就是我们切面没有动，只是构造的那个立体函数上下在动。

大家仿佛都有意避开了一些东西，我们的三维是咋来的，这里可以摊开了说，第三维是图像来的和先验速度为法线来的。

也就是之前我们只是一个平面的环，那么怎么变成立体的山呢？？？

环函数+图像梯度类信息+法线方向先验=三维的山。

这样我们应该就可以理解了，我们如何让图像控制曲线演变速度呢？用梯度信息（边缘梯度大）

如何控制演变方向呢？用最优方向，法线方向。（曲线沿法线方向变化最快）

这样就能理解了我们为什么要找F，这个F就代表了曲线变化的快慢，靠近边缘变化慢，远离边缘变化快。它加上法线方向，就表示了曲线的演变。

时间有限，先说到这里，欢迎来怼。