
添加时间:2024-04-22 14:20:29
生活中 ,许多问题都是由相互冲突和影响的多个目标组成。人们会经常遇到使多个目标在给定区域同时尽可能最佳的优化问题 ,也就是多目标优化问题。优化问题存在的优化目标超过一个并需要同时处理 ,就成为多目标优化问题。
多目标优化问题在工程应用等现实生活中非常普遍并且处于非常重要的地位 ,这些实际问题通常非常复杂、困难 ,是主要研究领域之一。自 20世纪 60年代早期以来 ,多目标优化问题吸引了越来越多不同背景研究人员的注意力。因此 ,解决多目标优化问题具有非常重要的科研价值和实际意义。
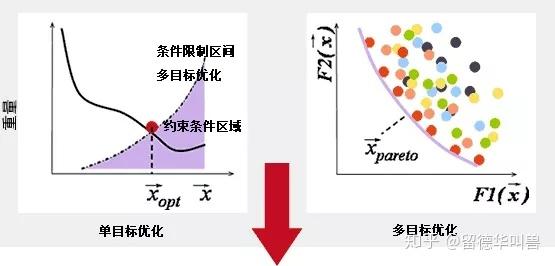
实际中优化问题大多数是多目标优化问题 ,一般情况下 ,多目标优化问题的各个子目标之间是矛盾的 ,一个子目标的改善有可能会引起另一个或者另几个子目标的性能降低 , 也就是要同时使多个子目标一起达到最优值是不可能的 , 而只能在它们中间进行协调和折中处理 , 使各个子目标都尽可能地达到最优化。其与单目标优化问题的本质区别在于 ,它的解并非唯一 ,而是存在一组由众多 Pareto最优解组成的最优解集合 ,集合中的各个元素称为 Pareto最优解或非劣最优解。
多目标优化问题用文字描述为 D 个决策变量参数、N 个目标函数、m + n个约束条件组成一个优化问题 ,决策变量与目标函数、约束条件是函数关系。在非劣解集中决策者只能根据具体问题要求选择令其满意的一个非劣解作为最终解。
多目标优化问题的数学形式可以如下描述[1 ]:
min y=f( x)=[ f1 ( x) , f2 ( x) , …, fn ( x) ]
n=1, 2, …, N
s. t. gi ( x) ≤0 i=1, 2, …, m hj ( x)=0 j=1, 2, …, k
x=[ x1 , x2 , …, xd , …, xD ]
xd_min ≤xd ≤xd_max d=1, 2, …, D
其中: x为 D维决策向量 , y为目标向量 , N 为优化目标总数 ; gi
( x) ≤0为第 i个不等式约束 , hj ( x)=0为第 j个等式约束 , fn
( x)为第 n个目标函数; X是决策向量形成的决定空间 , Y是目标向量形成的目标空间。gi ( x) ≤0和 hj ( x)=0确定了解的可行域 , xd_max和 xd_m in为每维向量搜索的上下限。
之前在Clemson的时候,机械工程系主任和我们(数学)系研究多目标优化的教授有紧密合作。
在汽车设计这个问题中,目标函数往往不是单一的。
例如汽车加速度和油耗是俩个互相矛盾的目标,这个时候,多目标优化就为决策者带来了选择的余地。
想牺牲多少油耗换取更高的加速度,是设计者可以在怕累拖最优的集合里自由选择的。
而这,就是多目标优化 VS 单目标优化(将多目标函数加权)的一个明显优势。
另一个多目标优化的应用案例:
文回答参考并节选自CSDN上的优秀文章:多目标优化详解 - CSDN博客
定义如下多目标优化问题,
通过非负加权求和把上面多目标优化转化为单目标问题,
对比多目标优化问题和单目标优化,最大的区别在于多目标优化问题是一个向量优化的问题,需要比较向量之间的大小,向量之间仅仅存在偏序关系,这就导致该优化问题的性质非常不好。
首先说一下我们平常遇到的优化问题严格来说都属于多目标优化问题,但是目前来说大多数的做法是把多个目标直接做非负加权求和转化为一个单目标的优化问题。所以这里要指出的就是直接处理多目标优化问题和通过加权求和的方式转化为单目标相比优势是什么?
多个目标之间必然存在矛盾,如何权衡这些目标,如果是用单目标加权的话,我们只能是调节权值大小,这样权值的确定其实是很难的,除了一顿实验没有什么太好的方法去确定,而多目标优化因为是直接求解多目标问题,就不存在确定权值的问题了。
各个目标之间量纲往往不统一,所以为了平衡各个目标之间的量纲,往往需要较大的权值 来平衡量纲。例如目标函数
的量纲相对其它目标函数就很小,所以为了平衡各个目标,就需要将
设置的很大,而如果
包含一点Noise的话,很大的权值
就会对整个目标函数产生巨大的影响。
加权求和的方式只能逼近帕累托前沿面为凸集的情况,如果多目标优化问题的帕累托面为非凸,则加权求和的方式就不能和原多目标优化问题等价,此时只有直接处理原多目标优化问题才能解决。
多目标优化问题的求解是会得到一个帕累托解集的,这个解集里边包含着很多的信息,例如可以产生一些对模型的可解释,可以分析多个目标之间的相关性等等。去年的机器学习顶级会议NIPS2018有一篇文章就是巧妙的将多目标优化的概念引入到多任务学习中,就是利用了多目标优化问题的这个性质。具体可参看我之前的回答 NIPS 2018 有什么值得关注的亮点?
说完了优势,那现在多目标优化的局限性是什么?为啥我们之前都是用单目标的比较多呢?原因比较简单,1单目标毕竟是比较简单的。2搞成多目标之后计算量要大大增加,这对于目前非常吃计算量的优化领域来说也很致命的弱点。看看多目标领域的顶级期刊的文章,搞个几千或者上万维的决策变量就是large-scale的了,可是在实际应用中经常会遇到百万,千万级别的优化问题。3多目标优化目前在处理2-5个目标还不错,如果目标数太多,其实目前也没啥太的好方法啦。4在业界的应用问题中,业务方需要你给一个明确的答案,而不是在一堆帕累托解集里边去选。
更多关于单目标和多目标优化可以参考
文雨之:【学界】数据+进化算法=数据驱动进化优化?进化计算PK 数学优化运筹OR帷幄专栏也会定期发布优化领域的科普内容和前沿进展
『运筹OR帷幄』大数据时代的运筹学坦白的告诉您,多目标优化对工业界也是很有意义,但它的问题在于:不容易出学术成果。
简单解释一下:
前面一些分享里多次提到多目标,这篇文章将开始这个主题的分享。
多目标这个主题的分享将会包括几部分:(1) 多目标的发展背景,(2) 为什么需要多目标,(3) 多目标的定义,(4) 多目标的实现,(5) 关于多目标在具体业务实践中的一些思考。
在推荐领域,多目标已经成为了业界的主流,各大公司的各种业务场景,基本都是基于多目标的框架来搭建推荐系统。
多目标在最近几年成为主流,和推荐越做越精细有直接关系。在互联网行业的红利期,用户在移动端的消费处于高速增长期,即使推荐系统粗糙,各种业务指标也很容易因为用户的自然增长而提升,这时候业务的效果提升,虽然离不开推荐系统的优化,但用户消费自然高速增长因素也起着非常重要的作用。在这种增量阶段,从业者对推荐系统做一些显而易见的改进,就可以带来明显的提升效果,所以对推荐系统的精细化也没有那么迫切。
随着互联网的用户自然增长红利逐渐消失,各大公司的推荐业务也相继进入到存量阶段,不再像增量阶段那样,用户的自然增长可以给业务带来持续提升,而是进入到另一种状态:各大公司都在存量的用户中吸引他们在自己的业务场景中消费。从业者发现按照增量阶段的改进方法,已经很难带来明显提升,于是开始“卷”起来了,朝着对推荐系统的精细化方向进行迭代和优化。
在推荐系统向精细化方向发展的阶段,多目标的研究和应用随之增多,和推荐系统的精细化相辅相成,可能是精细化的需要促进了多目标的研究,也可能是多目标的研究促进了推荐系统精细化,两者类似“先有蛋还是先有鸡”的问题。总之多目标的研究和应用,在业界成熟落地,从技术上促进了推荐领域的发展。
对推荐场景来说,好的生态,需要具备准确性、多样性、新颖性、惊喜性等多方面效果。(如何衡量一个推荐系统的好坏在《婷播播:什么是好的推荐,重新理解AUC》也提到过一些。)要让推荐系统同时具备上述的多种效果,单目标很难做到。
在单目标的情况下,很可能出现某一方面效果还可以,而其它方面效果很差,实际情况往往是某一方面的效果也很难做好。比如以点击率为单目标建模进行推荐,则往往容易准确性有一定保证,而多样性、新颖性等效果差,甚至准确性也难以做好,因为点击率高的内容,存在标题党或者封面党的问题,这样的内容用户很可能会点击,但点击后会很快退出,因为内容并不是用户真正感兴趣的。
推荐系统要达到推荐准确的效果,推荐用户真正感兴趣的内容,单目标也很难做到。用户不同的行为背后有不同的动机,代表了不同维度的兴趣出发点。用户点击表示有意愿消费,用户停留一定时长表示有兴趣,用户评论表示愿意和内容生产者产生联系等,一项内容如果能引发用户的正向行为越多,那用户对这项内容的兴趣也越高。但大多数用户的正向行为项数量是一两项,不会很多,因此当只使用单目标时,则很容易导致触发用户某种行为的内容占主导,而忽略了用户背后真实的兴趣,也不利于推荐的生态建设。
在具体场景中,用户的正向行为丰富多样,而一些正向行为之间存在一定的此消彼长的关系,比如当用户点关注后页面会进入到作者主页,则关注后用户则停止了对内容的时长消费,因此关注行为和时长之间存在拉扯。这时如果以其中一个为单目标进行推荐,则会对另一个目标有损,但推荐追求的是“既要又要”,只有多方面都兼顾到了,推荐系统才可能向一个好的生态方向发展,因此需要多目标来进行建模,从而尽可能地综合用户的多种兴趣维度,达到好的推荐效果。
多目标的应用,主要解决单目标的几个问题:(1) 单目标存在无法识别用户多维度兴趣问题,有误导风险;(2) 不同单目标之间存在“此消彼长”的关系,难以兼顾。在业务迭代过程中,多目标可以帮助推荐系统不断完善。
深度学习涉及的应用领域有多个multi相关的概念,除了多目标multi-task,还包括多域multi-domain,多标签multi-label,多类别multi-class等,虽然都包含multi,但具体含义区别很大。
multi-task
多目标multi-task是我们这个主题聚焦的问题,顾名思义,multi-task是学习多个任务,有多个分类或回归目标。不同任务可以有不同的样本或特征输入,也可以基于相同的样本和特征。例如对一个样本,可以有是否点击、是否评论、是否关注、停留时长等多个建模目标,根据不同的目标定义,既可以是分类任务,也可以是回归任务。
multi-domain
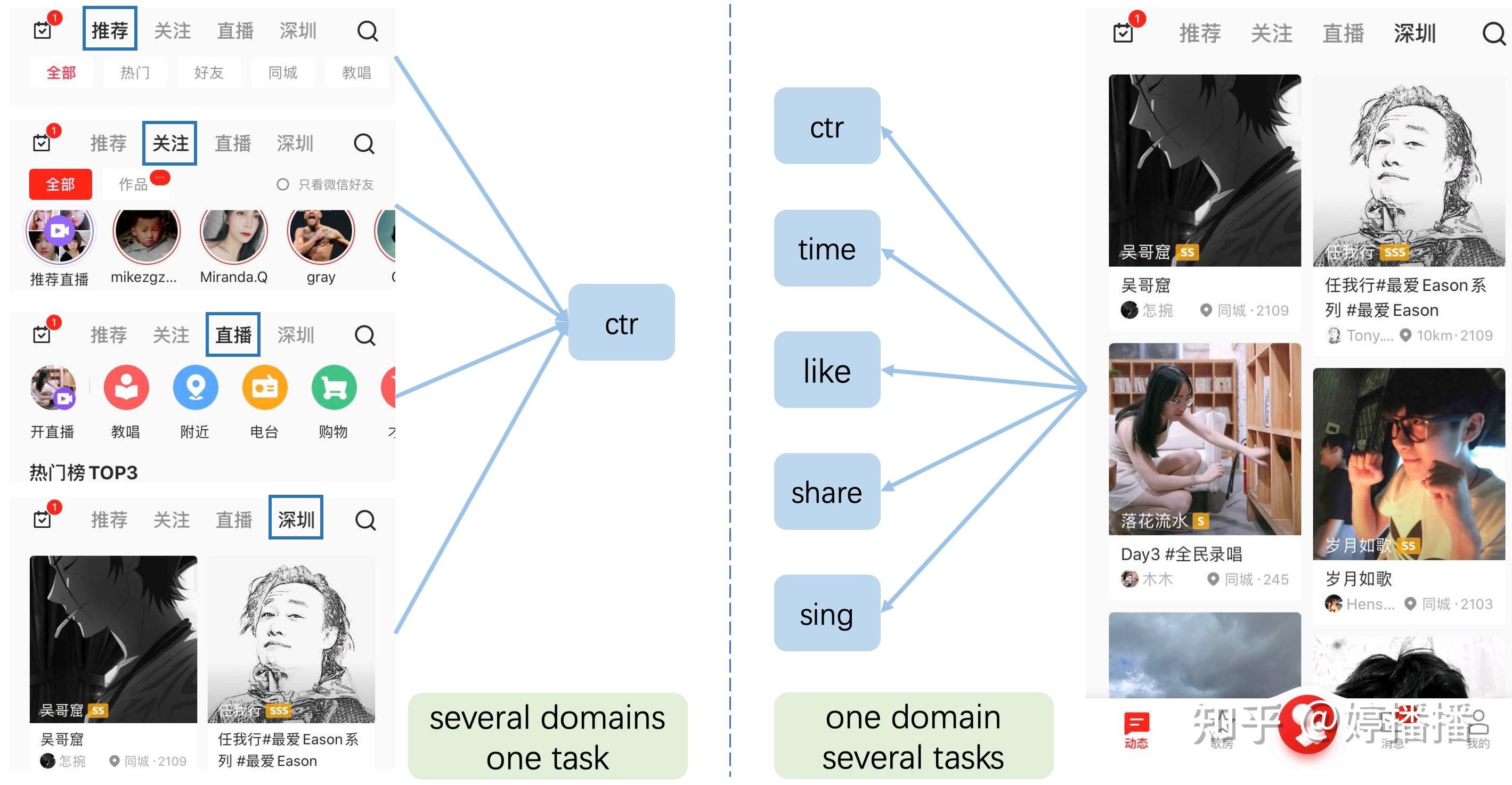
多域muti-domain表示对不同域的样本进行建模,在推荐领域往往对应不同场景的样本。例如在热门内容中会插入广告,那么内容和广告就形成了两个域,而用户在消费的时候,由于广告是接到某个内容后出的,两者存在一定的上下文关联,因此在不同域进行建模时,可能会使用其它域的数据来更好捕捉用户兴趣。再比比如app不同的入口,也是不同的域,如图1左边所示的推荐、关注、直播等多个tab,就是多个域。
图1左边表示的是multi-domain,task是是相同的,右边表示的是一个domain中进行不同task的建模,也就是multi-task。
multi-label
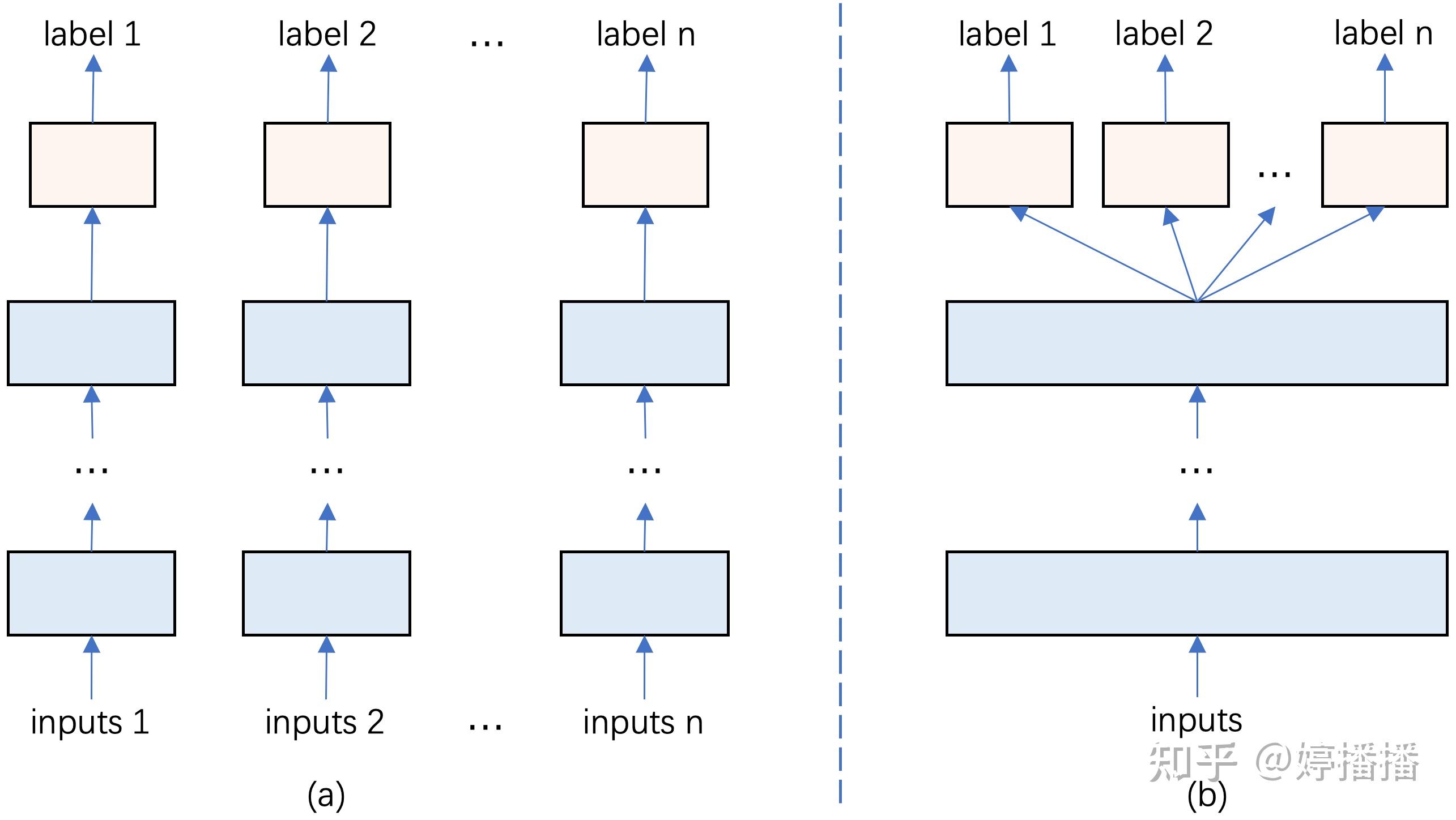
多标签multi-label表示对样本进行多个维度的分类,是multi-task的一种,但区别在于,multi-label是基于相同的样本和特征进行建模,multi-task可以每个任务对应一个模型,每个模型有各自的样本和特征,最后对不同task预估进行融合,得到最终结果。同样以推荐场景为例,可以有是否点击、是否评论、是否关注等多个label,当建模过程是基于同样的样本和特征得到多种label时,这时候既可以认为是multi-label,也可以认为是multi-task,如图2(b)所示;而当建模过程不同label对应不同的样本或特征进行建模的,则是multi-task而不是multi-label,如图2(a)所示。
multi-class
多分类multi-class表示分类结果有多种选项,不同于二分类只有两种可能。比如对一个人的年龄进行多分类问题,则分类结果可以是[少年、青年、中年、老年]几种类别中的一种。
多目标的建模和单目标大体类似,两者本质都是在解空间里找最优解,只是多目标需要考虑的目标更多,比单目标找最优解更复杂。多目标基于自身的特点,在模型结构、损失函数等方向上发展出一些方法。
3.2.1 task融合
多目标中每个task具体定义,需要根据业务需要来制定。对一个推荐场景来说,除了考虑ctr,还会考虑用户消费时长,用户和内容生产者的互动行为,包括点赞、评论、转发等。
multi-task建模后一般需要task融合,对不同的task预估综合考虑,得到最终结果。task融合依赖于融合公式,对融合公式中的参数调整可以直接影响不同任务对最终结果影响的重要程度。在实际落地时,需要根据具体业务的特点和需要对融合公式设计和调整。
3.2.2 模型设计思路
multi-task的模型设计不断被改进,其核心在于平衡多种任务的共性和特性。
早期的多目标采用的是多个目标单独建模的方法,也就是图2(a)的方法,这种方法简单,但存在以下问题:(1) 计算量大,每个task的网络结构基本相同,都需要经过一遍网络计算,重复性操作多;(2) 有的目标样本稀疏,模型预估准确性低;(3) 不同task基于不同的表征计算,相当于在不同标准进行预估,增加后续多task预估的融合难度。因此衍生出基于同一个特征空间的模型结构设计,如图3所示,所有目标的预估是在相同的特征空间下进行。
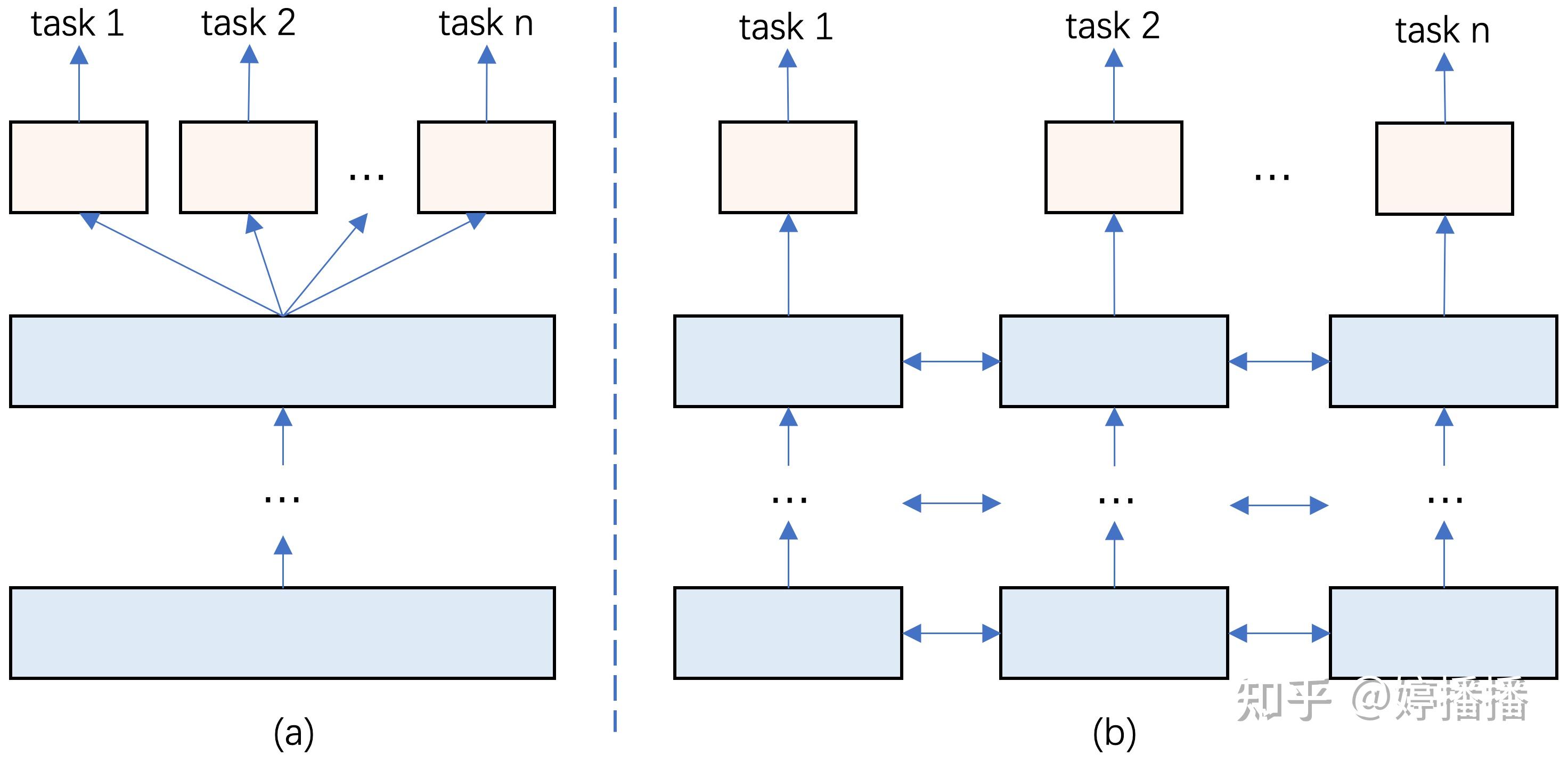
图3(a)所示的模型结构为hard参数共享,即所有任务共享隐藏层,最大程度地保留了任务之间的共性,而各个任务的特性则没有得到重视。soft参数共享的网络结构如图3(b)所示,每个任务有自己对应的参数,不同任务之间的参数通过一些约束,使其在训练阶段受到一些限制,这种方法突出了每个任务的特性,而减小了任务之间的共性的重要度,同时参数量也比较大。
后续multi-task的模型结构的改进思路,是结合hard参数共享和soft参数共享这两种结构的优点,使模型在学到所有task的共性的同时也学到其特性,从而提高推荐准确性。
多目标的实现包括模型结构、损失函数等一些方向,下一篇将介绍多目标的一些典型模型结构。
推荐系列文章:
推荐模型结构-特征交叉
推荐基础知识点
工具
工作相关的内容会更新在【播播笔记】公众号,欢迎关注
生活的思考和记录会更新在【吾之】公众号,欢迎关注
吾之系列文章:
今天我想介绍一下我的第二篇博士论文,内容是关于多目标问题的优化。我会用尽量少的公式,尽量通俗的语言来介绍我的idea。
优化的字面意思就是选择某个决策,让某个目标尽量好/高。在这里考虑目标outcome为Y,Y是一个关于连续变量A(比如某种药物剂量)的函数。如果我们能够画出Y v.s. A的变化曲线(dose response curve,当然,这如何寻找是另一个领域的问题),那么我们就能轻松的优化Y,也就是找到这条曲线的最高点。在这里,当 时,Y达到最高点。
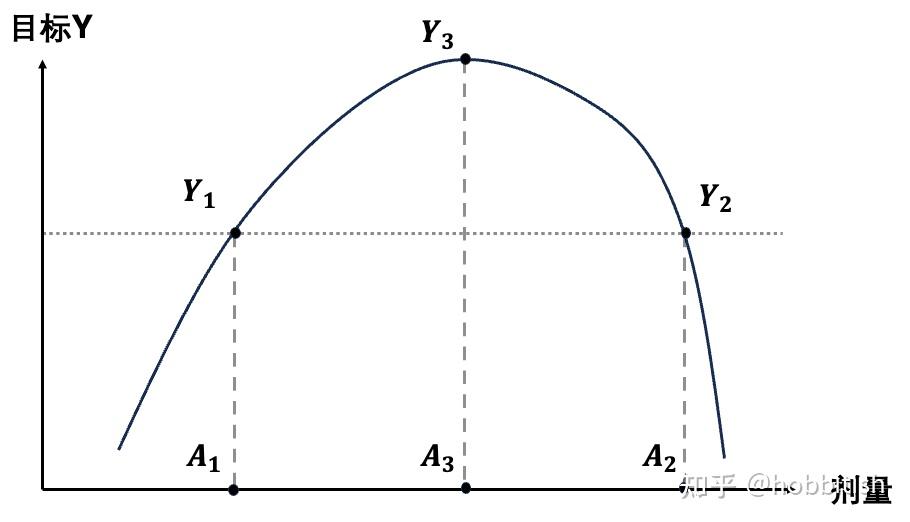
以上情况是最简单的单目标优化,非常的显而易见。但当我们把问题拓展到多目标优化时,如何解决问题就不再那么显然。
举一个很简单的例子,考虑语文数学两门学科,班主任想评出最优秀的学生为三好学生。但尴尬的是,两名候选人,小明语文100,数学90,小红语文90,数学100。两者齐头并进,不分高低,各有优劣,此时我们该如何定义什么是最优秀?
在临床实践中,几乎所有的问题都存在这样的情况,比如:一,是药三分毒,药重了,有副作用,药清了,治不好人,怎样下药才是最好?;二,有人觉得好死不如烂活着,但生命的长度和生命的质量往往不可得兼,高质量的生活3年和苟延残喘20年,孰优孰劣,尚未可知。
对于多目标优化,一个最容易想到的方法(也是数学家最常用的方法,即将未知问题转化为已知问题),是将它简化为单目标优化:
在这里,我们引入了一个新的效用函数(utility),直观的说,就是引入了一个各科成绩的“总分”。但这里总分并不是将两个成绩直接相加,而是采取了一定的权重。比如,这次三好学生的评选更侧重数学,那么最后总分为可能是0.7数学+0.3语文。在这种情况下小明总分为93,小红为97,小红当选为“三好学生·数学之星”。
当然,这个方法有很多不足之处,比如,这里0.7的权重是如何选取的?是不是班主任因为数学老师的身份搞黑幕?在实际情况中,这里的权重往往是未知的,或许我们能够借助专家意见给出一个推荐值,但这毕竟不是很有说服力。
另外,不同人对不同目标的偏好可能是不同的(这里我们有时叫“权重”,有时叫“偏好”,都是一个意思,一个主语是目标,一个主语是人)。比如,年轻人治病时,可能更侧重生活长度,而老年人治病时可能更侧重生活质量(毕竟本身也没几年预期寿命了)。语文老师和数学老师对此次三好学生评选中,不同科目的权重肯定也有不用的看法。换句话说,不同个体存在偏好差异(preference heterogeneity)。
因此,我们更希望使用数据驱动的方法,通过观察性实验来学习这个权重/偏好,而不是通过专家拍脑袋定一个数。这里我通过一个例子来体现这个方法的可行性:在开车时,我们事实上是同时兼顾了多个目标的,既要开的快一点,又要和其他车保持距离等等。但我们开车时,脑子里想的肯定不是以上公式,而是直接根据经验,下意识地做出一些反应。我们也很确信,我们做出的这些行为,就算不是最优的(optimal),也至少是次优(sub-optimal),也就是说,至少比随机行为(拴一条狗来开车)要强。那么,我们的行为就蕴含着“对于多个目标的偏好”的信息,而只要数据中存在信息,我们就有可能去学习它!我们管这个叫“专家信息学习”(expert information learning)。在开车的例子中,人类司机就是专家(不必是最优的赛车手,只需会开车即可),而被观察到的数据就是开车的行为,多目标则是开车的速度,离其他车的距离等等。

最后,我们还想将问题拓展到连续剂量上去,比如想找出药物的最佳剂量(连续值),而不是简单的吃药不吃药(离散值)。
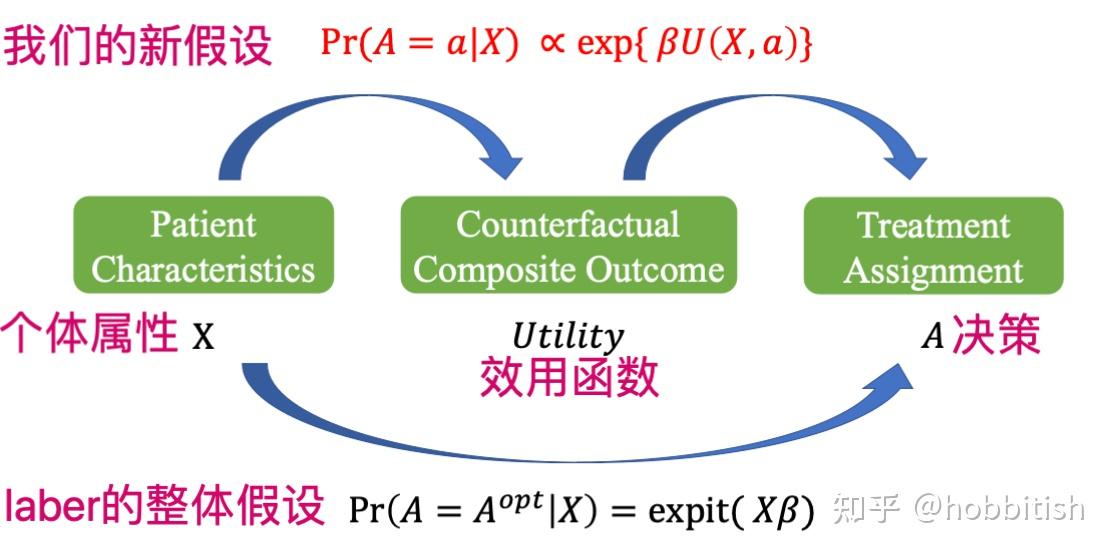
Luckett et. al., 2021 的文章提出了一个有意思的假设:对于离散的行为(比如yes, no),在观察性实验中,“观察到的行为=实际最优行为”的概率取决于不同人的属性(characteristics,比如男女,年龄)。通过这个假设,我们进行似然估计并且计算不同目标的权重。
但其局限是,只能用于离散行为,而不能作用于连续变量(比如药物剂量)。同时,我认为这个方法只是一个全局的/整体的估计(marginal),忽略了很多有用的信息,比如观察到的行为(A)和效用函数(Utility)之间的关系。
这个想法也很简单粗暴,既然我们不知道权重,那么我们就分两步来,第一步,估计权重,第二步,有了权重之后,就能做单目标优化了。至于怎么估计权重,那就干脆直接问每个人他们的偏好是啥,或者让他们填个问卷调查表,然后来估计。
这个方法的问题是,他实际上将一个难题转化为了另一个难题:事实上,怎么证明你的问卷调查能真实反映个体的偏好,是一个很难解决的问题。同时,这个方法不能引入专家信息,完全没有用上我们观察到的数据,比如专家在实际中是怎么权衡药量的,造成了很大的信息浪费。
这个经常用在自动驾驶的学习中,也是想要去学习专家信息(人类司机)。但他的问题是,他认为目标函数/效用函数是个固定的东西,不能引入“不同人可能存在不同偏好”的可能。
帕累托方法可以说是最有名的一个处理多目标优化的方法,可能有一大半的paper都是用的这个idea,实际中也基本用的这个。它的想法是,我不找出最优的,我只是把“绝对不是最优”的去掉,然后剩下的都叫“帕累托最优”!这个想法听起来有点脱裤子放屁,但在解决一些问题时还是蛮有用的。比如之前的三好学生评选中,除了“小明语文100,数学90,小红语文90,数学100”,还有个小刚语文80,数学95。虽然小明和小刚还是很难说谁比较好(小明语文高,小刚数学高),但很明显小红每一科都比小刚好,小红dominate(翻译应该是支配,但我愿称其为“碾压”,否则有点怪怪的)了小刚。所以小刚连候选人的资格都没有了(不是帕累托最优)。
实际中这个方法可以有效地减少候选人名单。据一个极端的例子,每个决策有20个小决策,每个小决策都是yes or no,那么一共会有2的20次方,大概是10的六次,100万个不同的决策。但用帕累托最优的想法和一些机器学习的算法,我们可以挑出100个候选人,这大大提升了效率!至于你问最后这个100个候选人选谁,那就不关我事了,老板来拍板,我不背锅 。
由此我们也可见帕累托的一个缺点,就是它不能给你一个唯一性的决定,往往还是要人为的决策。但对于算法而言,自动决策,好!主观决策,坏!想象一下你的智能手环,如果每个手环给出的提示,最终还是由客服决定的,那将是不可接受的成本。
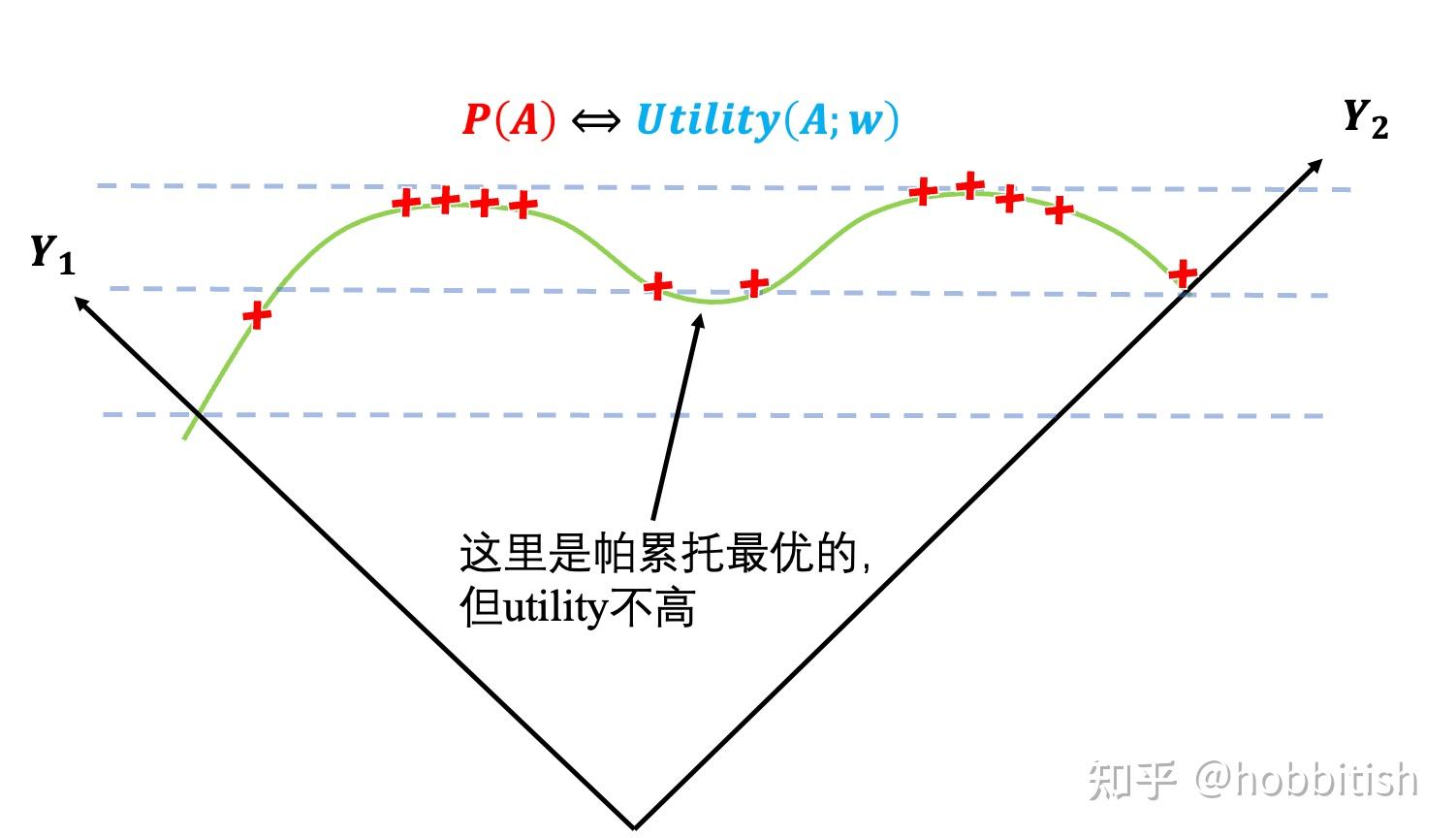
另外一个致命缺点,就是这个想法对于连续变量无用!在临床上,医生们有一个结论有很强的信念:随着剂量增加,治愈率(Y2)一直增加,安全性(Y1)一直降低,那么在这种情况下,所有剂量都是帕累托最优,它只是优化了个寂寞。
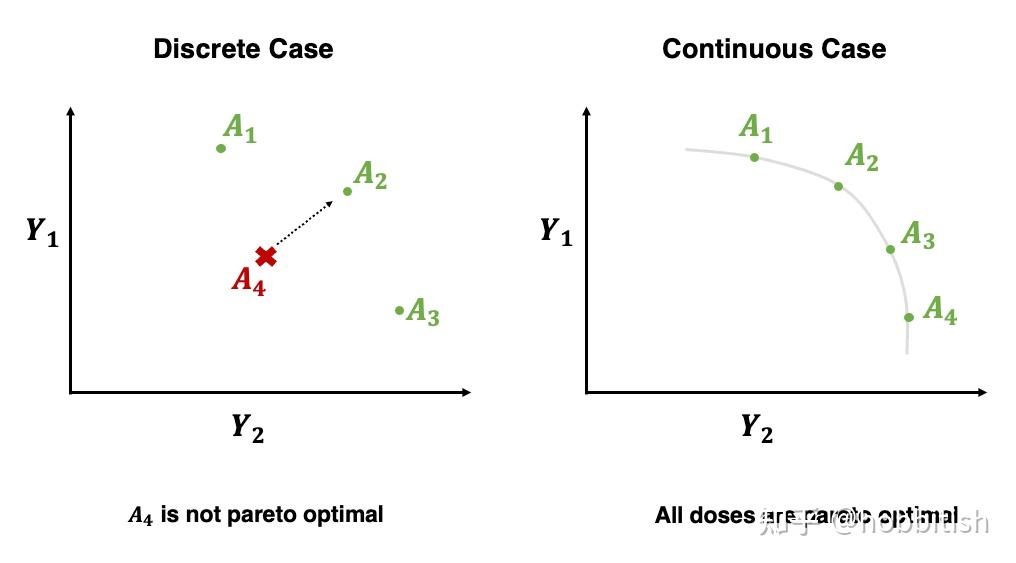
以上就是这个多目标问题的一个回顾,我们想要提出一个新方法来同时达到:1,专家信息自动学习;2,考虑个性化治疗/差异化的偏好;3,能做用在连续变量上。
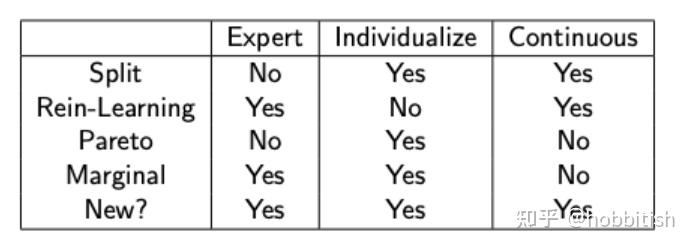
先还是简单介绍一下定义:

受之前luckett的paper启发(“观察到的行为=实际最优行为”的概率取决于不同人的属性X),我们提出新的假设:
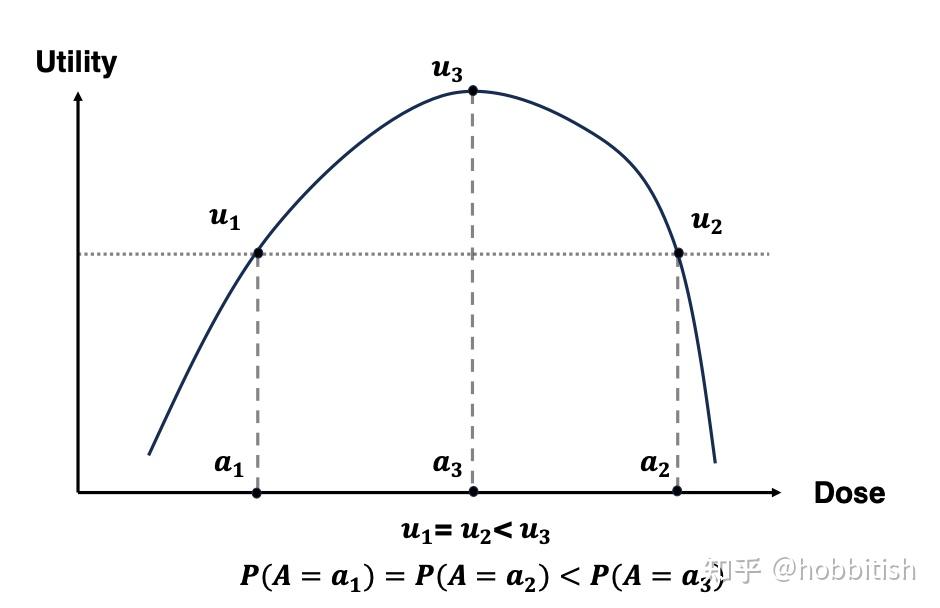
在上面这张可视化图中,让我们首先假设我们已经找到的效用函数Utility和剂量A之间的关系:
你可能会问,那我们要怎么画出以上这个曲线呢?构造效用函数utility所需要的目标权重不是未知的嘛?那么接下来我们再看:
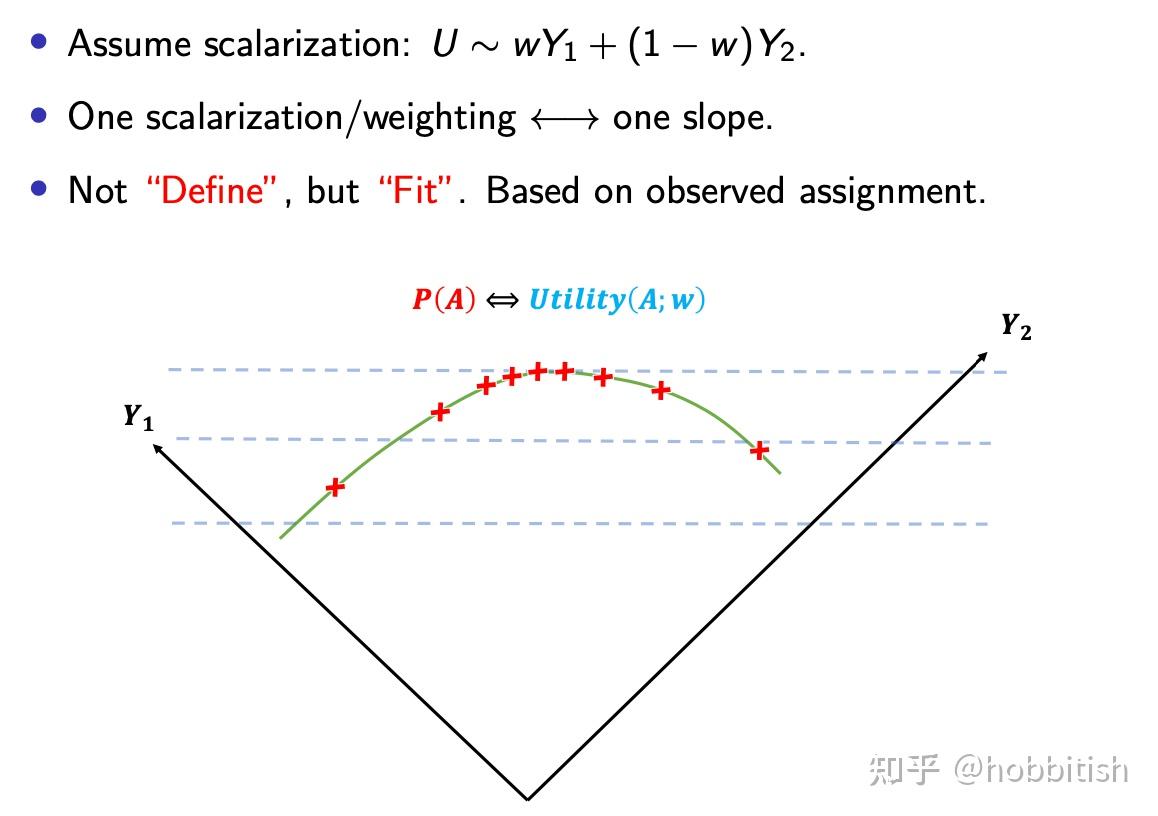
理想的情况应该是,观测到的决策(红叉)分布在等高线更高的地方,因为专家们想做尽量好的决策!我们可以将上面这个图再次转变一下,使其更容易理解:
如果我们找到了正确的权重的w,那么这两条线应该是完全吻合的!而这提供了如何找寻正确权重的方法:“尝试不同的权重w,当两条线吻合时,那就成功了”。
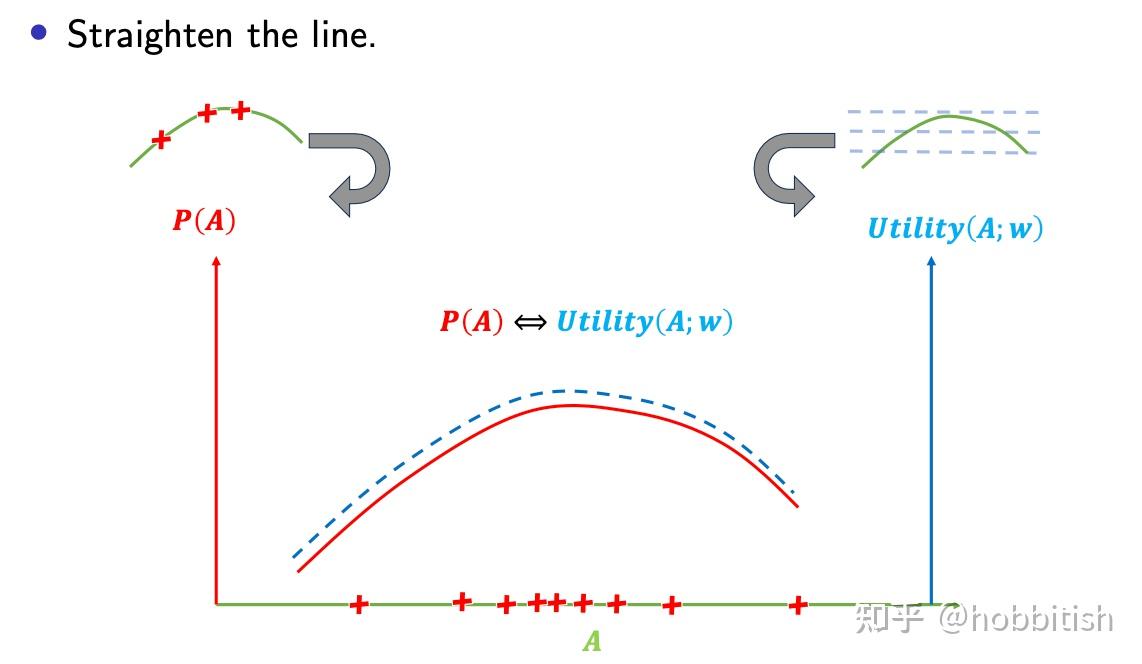
那么接下来,我们将上面的直观想法,翻译成数学语言:






太多的simulation结果我就不放在这里了,感兴趣可以看我的paper。这里只简单比较一下我的方法和laber的方法。因为它们的方法只能适用于离散决策,为了照顾它们,下面的模拟我们也只用离散决策的情况。对于不同算法,它所依赖的假设是至关重要的,我们将依次查看不同算法在不同假设下的效果。
在laber的假设下,我们的模型(土黄色)和laber的(红色)大概打个五五开吧。
另外几个方法是观测到的决策(绿色),只考虑Y1的决策(蓝色)和只考虑Y2的决策(粉色),总的来说都不咋样。
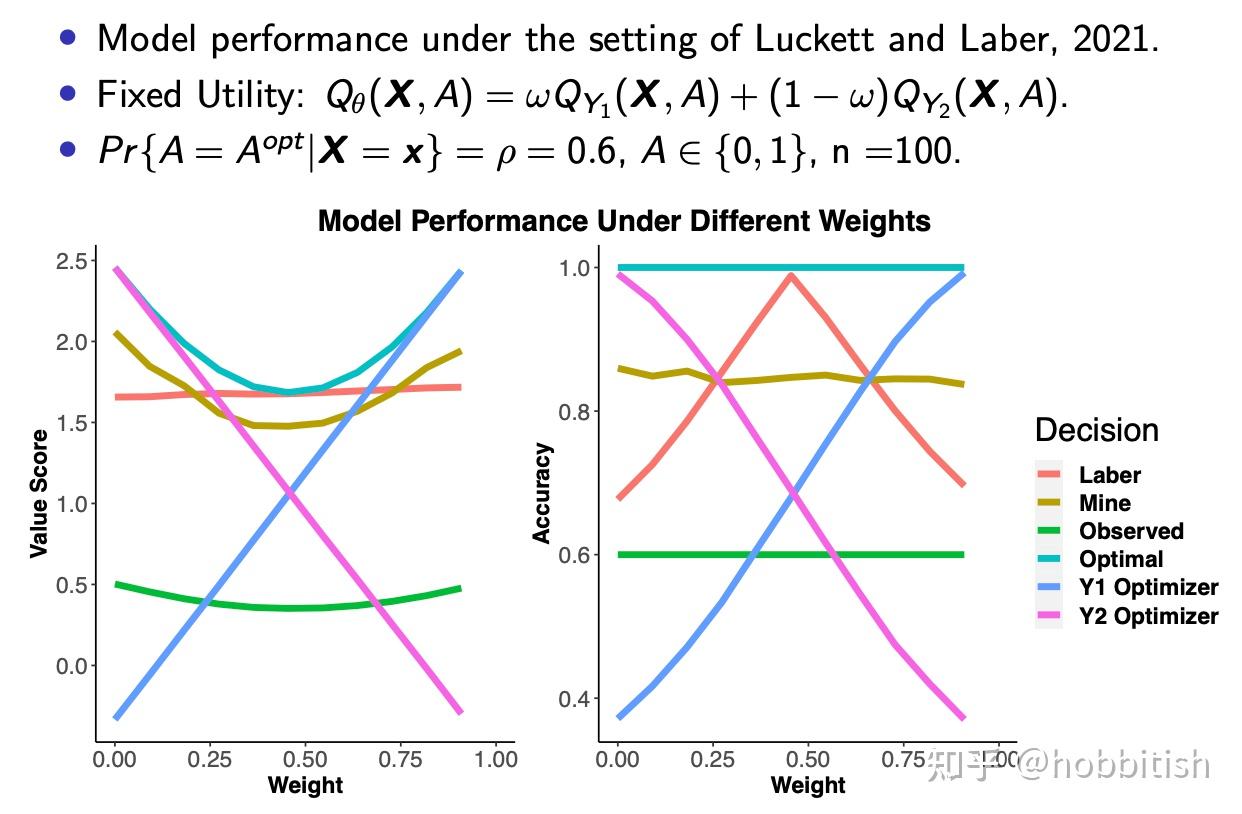
这里我们可以看到,我们的新方法(黄色)几乎碾压laber的(红色),仅在真实权重值w非常接近0.5是,laber的略微好于我们。
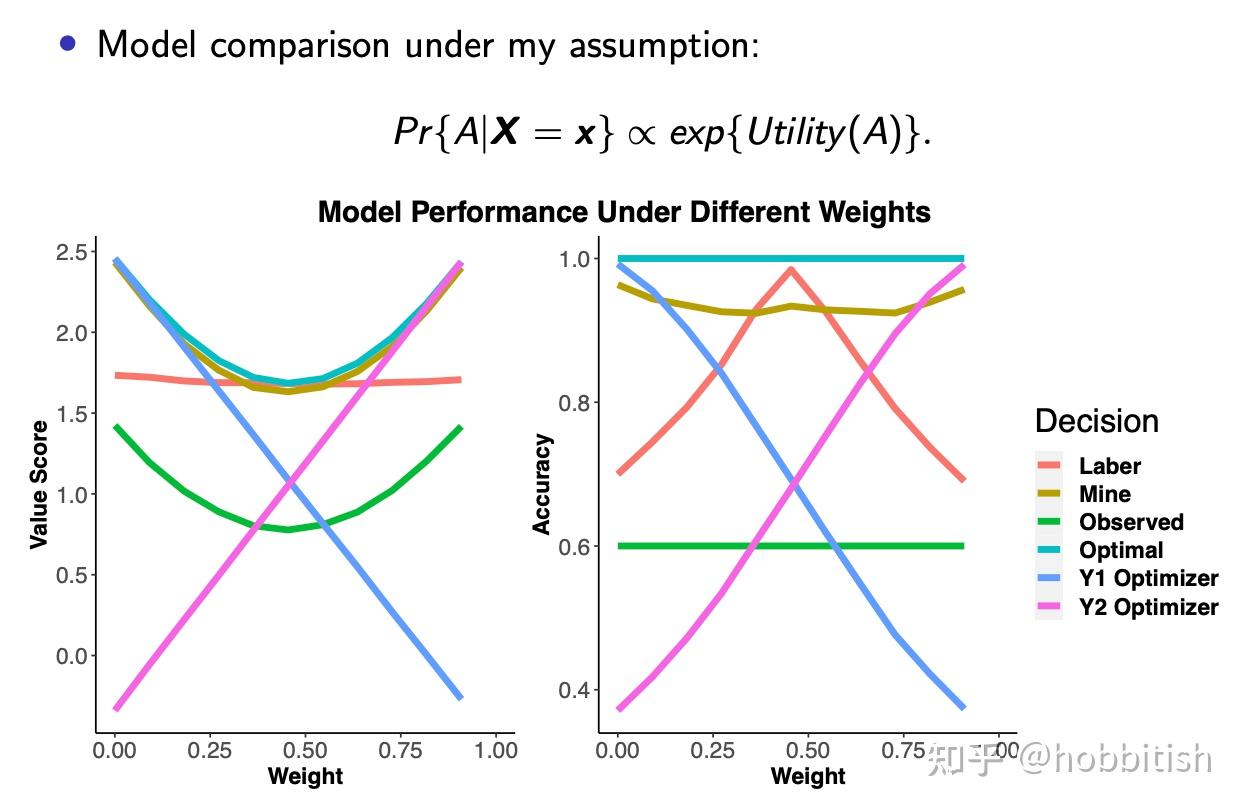
总的来说,我们方法,即使在其他的假设下,依然有很稳定的表现(甚至和laber它们自己的方法五五开)。下面是两个模型“信息流动”的可视化。
laber的论文直接模拟了个体属性到决策的关系,忽视了其他可能存在的机制。
我们认为,医生在诊断时,并不是仅依赖于你的性别,年龄等特征(当然它们是有用的),他其实是在心里模拟了,你吃不同剂量的药会有怎么样的结果,然后挑选了一个他认为能带来好结果的药!因此,效用函数(好结果)与决策(药量)的关系是十分重要的!
另外,一个有意思的点是,我们假设了观测到的决策至少是次优的,虽然这个假设很弱,几乎总是对的,但我们能不能去验证他呢?答案是可以的!
我们前面提到了,参数beta对应了观测到的决策的优秀程度,beta=0对应随机决策。那么我们只需对beta=0进行假设检验,只有当beta显著大于0时,才进行下一步分析!而这也是十分重要的,因为我们不可能从随机决策中获取任何信息!
同时,这个方法同样适用于多目标优化,不仅仅是两目标优化!
总的来说我还是很喜欢我的这篇paper的,虽然他没有很复杂的公式推导,但我自认为这是idea非常新的一个突破,目前我还没有看到其他对于多目标优化的新思路,大家更多还是在帕累托最优的一亩三分地死磕。欢迎大家讨论私信,以及引用我的文章(已经上传到arxiv啦)!Adaptive Weight Learning for Multiple Outcome Optimization With Continuous Treatment
答:1,帕累托不适用在连续变量上,比如医学上,对于某个药物的剂量,剂量增加,治愈率永远增加而安全性永远降低,所有剂量都是帕累托最优,因此这个方法没有任何用。帕累托适用在离散变量上,通过寻找帕累托前沿来降低决策数量。2,帕累托不会给你唯一结果,最终还是要人从帕累托前沿中选出一个结果,不能用在自动化设备上。
答:本文重点在于,假设“观察性实验中专家给出的决策依赖于实际的效用函数”,至于效用函数是什么,你可以用任何形式。这里我们仅使用的最简单的线性+参数形式(linear + parametric)。我现在正在做的另一个idea是使用semiparametric model,让效用函数可以是两个目标的非线性函数。你可以根据学科背景使用任何你想要的形式,比如不用probability而用odds等等。
有读者提到,我们想观察不同目标之间的张力,比如Utility,Y1,Y2之间的关系。我们的方法同样能做,把Y1,Y2的加权和换成Utility=f(Y1,Y2),一个任意,非线性函数,然后用非参的方法来估计即可,所有流程依然保持不变。我觉得这个在这篇文章的基础上就显得十分trival了,所以暂时不打算做这个。
另外,这个paper是受实际医学例子启发的,医生想要一个直接的,对于毒性和治愈率的权重,让他们能直接应用在实践中,所以我们用了加权和的形式。
在我看来,多目标优化中,不同目标的个性化偏好/重要性/权重是只有病人和医生本人知道的(就假设在医学领域吧)。即使我们站在上帝视角,完美地知道了不同目标与决策之间的关系(dose response curve),我们依然无从知晓病人的个性化偏好,因为它们完全就是两个不同的东西!而个性化偏好这部分信息,只能由“观察性实验中,经过医生和病人的交流协商,最后做出的决策”所反映!这也是我个人不喜欢帕累托优化的一个原因:的确,它没错,但它少利用了一部分信息,而天下没有免费的午餐,它终究是无根之水,不可能凭空计算出病人的真实偏好。
有一位朋友在评论区提到“非凸情况下一条切线跟目标函数分布图(绿线)甚至可能只有两个交点而同时Pareto解集的测度严格大于0。”如果我们试图用不同切线找出不同帕累托最优,那么在非凸的情况下自然计划泡汤了。但我们这里并不是这么做的,我们这里的蓝线,只是效用函数的等高线,并不是尝试用它去“切”它。只要我们找到这样斜率的等高线,使得“高的地方红点密集,低的地方红点稀疏”,那么我们的方法就能找到正确的权重/斜率,与凸性无关。至于你问问什么要用这样的效用函数(两个目标的加权和),见2.
很多人会有个误区:你这个结果怎么衡量?跟帕累托前沿的结果吻合吗?但我要强调的是,帕累托前沿并不能定义“好”/“优”,它只是“不差”!在我们的假设中,观察性实验中,专家给出的“次优决策”才定义了什么是“优”。如果没有观察到的数据,没有人能定义什么是“优”!
换句话说,我们想做的是模仿专家行为,比如自动驾驶中,电脑想模拟人类行为,只不过在估计出参数之后,我们不再需要随机性,不要次优,每次都选我们估计出来的最优。
这篇文章,我们根本不care Pareto 前沿 。
最后这是我最近的一些想法,我觉得多目标问题应该分为两种:
第一种其实是不存在最优决策的。比如汽车由不同零件构成,每个零件都是不同的决策,我们的目标其实是找到“不错”的组合,且并不存在“最完美的汽车构造”,而帕累托最优就是应运而生的,它应该也是最恰当的解决方式了。
第二则是每个人心中的的确确存在某个偏好,只是无法量化,通过医生与病人协商后作出的次优决策,我们可以一窥其貌。因为偏好是客观存在的,所以也就存在最优决策。而这也是我们这篇文章的立足点。比如校长评三好学生时,心中有个标准,如语文30%,数学70%,且他会给出不同人评价“不行”“不行”“不错”“很好”“很好”。我们根据每个人的分数分布,和校长对应给出的评价,用我们的方法得以估计校长心中的那个标准!而这是帕累托最优无法做到的。
更一般的来说,尽管它俩有共同的名字“多目标优化”,但是帕累托是无监督学习,而我们这个带监督学习吧,两者还是有区别的。我想这也是大多数人会误解我们方法的地方。
地址:海南省海口市电话:0898-08980898传真:0898-1230-5678
Copyright © 2012-2018 耀世娱乐-耀世注册登录入口 版权所有ICP备案编号:琼ICP备xxxxxxxx号